Limitation in using random digit span as a measure of cognitive load

The previous activity used a digit span task to demonstrate that human working memory has a capacity of somewhere between 4 and 9 elements.

For the previous activity this means that:

1. when the total number of digits to be remembered is four then the task is trivially easy for most people.
2. when the total number of digits to be remembered is eight then the task is achievable for most people if they exert ‘some mental effort’.
3. when the total number of digits to be remembered is sixteen then the task is beyond capacity for most people.

In many ways, however, this task is artificial. People are rarely required to memorise sequences of random digits. After all, even telephone numbers and post codes may have an underlying logic.

Most of the information that we are required to learn in our lifetime is far more complex than a simple sequence of objects (whether they be digits in a telephone number, or items on a shopping list). Content areas such as mathematical calculus, biochemistry and computer programming are considered to be "difficult" to master. One of the reasons for this is undoubtedly the sheer volume of information that must be acquired (and built into schemas) before an expert knowledge base is held in the area.

But there is another critically important feature that is evident in these content areas: that of 'high element interactivity'.

Element interactivity

Element interactivity is defined as the degree to which the elements of some to-be-learned information can, or cannot, be understood in isolation.

If individual elements can be comprehended (and learnt) in isolation from other elements, then by definition, they are not interacting with other elements.

In contrast, if the content is such that several elements need to be comprehended (and learnt) simultaneously because they interact with each other, then it is high in element interactivity.

Some examples will assist in demonstrating the dynamics of element interactivity.

Example 1: Foreign language

Consider the task of learning a foreign language. Most people can quickly learn some simple, everyday words, but will have difficulty in generating grammatically correct sentences, even when all of the words used in the sentence are known.

Vocabulary is an example of low element interactive material. Although there may be literally thousands of words to be learnt, most words may be learnt in isolation to all of the other words.

To build sentences that are grammatically correct, however, one must attend to all of the words within the sentence at once to enable attending to syntax, tense, verb endings and so on. Grammar is an example of high element interactive material because to learn it, many elements must be considered simultaneously as they interact with one another.

Example 2: Chemistry

In areas such as chemistry the symbols of the periodic table are low in element interactivity and can be learnt in isolation from one another. However, their organisation within the structure of the periodic table is based upon their chemical form, weight and valency and so need to be considered together. Balancing chemistry equations, by definition, needs the consideration of valency for multiple elements and the nature of the associated chemical reactions. It is the high density of high element interactive content that makes chemistry “complex” and to acquire a reputation by many students as difficult.

Example 3: Puzzles

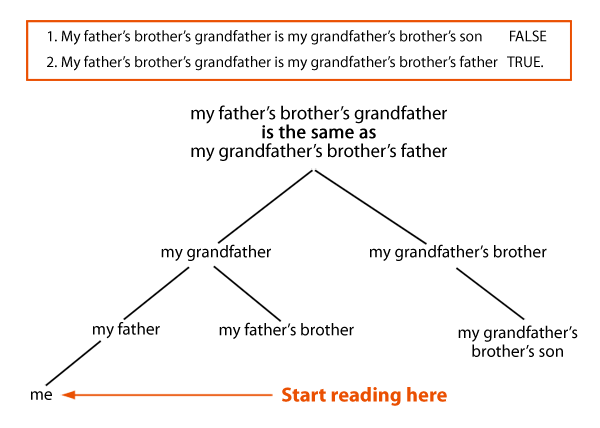
By way of a further example, attempt to determine if either of the following statements could be true.

   1. My fathers' brothers' grandfather is my grandfathers' brothers' son.

   2. My fathers' brothers' grandfather is my grandfathers' brothers' father.

Although each of these statements requires only a few elements (the people involved) to be considered, the activity is extremely difficult because there is a need to also attend to the relationships between the elements.

Element interactivity in this example is quite literally about how the different people are related to one another. Element interactivity is about relations between elements!

It is the high level of element interactivity contained in each of the propositions that make the task “complex” and difficult to solve.

As a consequence of the high element interactivity, the cognitive load induced may exceed the resources of working memory.

The cognitive load associated with this material can be greatly reduced if some of the information is presented pictorially. Elements which interact with each other often have the potential to be presented in pictorial form, where the picture itself holds (and conveys) some of the information about relations, removing the need for it to be held in working memory.

A diagram can also provide an extension to working memory, thus freeing resources to be given to the task of analysing features of the two propositions.

If, in looking at the diagram below you ‘touch’ a point with your finger to hold that as a reference while you attend to other aspects of the question or the diagram, then you are physically interacting with this as a memory aid.

The partial family tree presented below shows that statement 2 is logically possible.

High element interactivity and "combinatorial explosion"

Element interactivity produces combinatorial explosion.

By way of example, consider three elements that need to be learnt called ‘A’, ‘B’ and ‘C’.

If each of these elements interacts in some way with each of the other elements then the relationships ‘AB’, AC’, and BC’ also need to be attended to.

There is also the three-way interaction “ABC”.

This enumerates to a total number of seven distinct items that need to be cognitively manipulated.

In situations where there are just three elements, but where there is a full set of pair-wise interactive relationships, plus the three-way relationship, then the new information imposes a cognitive load that is roughly at our bounds of working memory capacity.

It should be noted that there are many three-factor relationships that people need to learn. Common examples in mathematics and science include ‘area = base x height’ for rectangles, and ‘F =ma’ for kinematics.

In learning a foreign language such as French a verb, the tense and aspects of gender of objects may all need to be considered to construct sentences because all of these elements interact to determine grammar. By way of contrast, note that some languages, such as Bahasa Indonesian, do not contain verb conjugation, and do not assign gender to objects, and this helps to explain why Bahasa Indonesian is considered easy to learn as a foreign language.

New information that consists of four elements; A, B, C, and D will yield the set of pairwise interactions of AB, AC, AD, BC, BD, and DC. It will also yield the set of three-way interactions of ABC, ABD, ACD, and BCD, and lastly, the four way interaction of ABCD. This totals to a set of 15 items of either individual elements, or some aspects of interactions between those elements. This is an example of 'combinatorial explosion' where the number of possible combinations between elements increases much more rapidly than the increase in the number of base elements.

Element interactivity impacts upon cognitive load significantly.

The evaluation of working memory capacity to be seven plus or minus two (Miller, 1956) is only true for attending to non-interacting elements.

For information that involves a high level of element interactivity the total number of individual elements that can be attended to simultaneously, while also attending to all aspects of element interactivity involving these elements, will be significantly less than seven.

In the analysis presented here, as few as four elements, each of which interacts with each other element, is likely to induce an intrinsic cognitive load beyond working memory capacity.

Next: The elements of working memory

References

Sweller J; Chandler P, 1994, 'Why Some Material is Difficult to Learn', Cognition and Instruction, vol. 12, no. 3, pp. 185 - 233, http://dx.doi.org/10.1207/s1532690xci1203_1