Subgoals
Subgoals subdivide a problem solving task down into a series of smaller problem solving tasks.
Providing subgoals to learners focuses their attention on structural aspects within a problem solving activity and reduces the number of alternative moves that they must consider.
When a series of subgoal provided problem solving activities is presented, the number of subgoals presented is truncated as the learner's schemas develop. This provides the learner with an increasing number of structural steps to complete, applying their developing knowledge base.
The subgoals are scaffolding which is gradually removed as learners gradually acquire schemas.
When presenting problem solving activities, include subgoals to provide guidance to structural aspects of the problem solution.
When a series of subgoal provided problem solving activities is presented for a similar problem type, gradually remove the number of subgoals provided as a learner progresses through the sequence.
The first subgoals to remove are those that provide the least important guidance. Subgoals should be increasingly removed through such a ‘least importance removal’ process.
When the content area is of higher complexity, or when the learners' level of expertise is lower (or both), provide a higher number of initial subgoals and gradually remove the scaffold provided by the number of subgoals.
For problem solving activities, include subgoals to focus attention on important structural aspects of the solution path.
When a series of problems is presented as the learner progresses through the series, gradually reduce the number of subgoals presented, thus requiring the learner to increasingly complete the problem solution.
Gradually remove the number of subgoals presented throughout the series until all subgoals are removed.
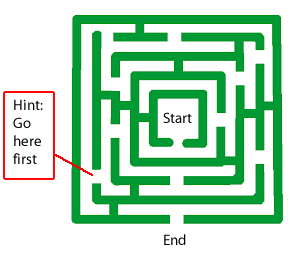
Here is a maze.
Begin in the middle, and find your way out.
A hint is provided...which is a sub goal.
This, visually, is how sub goals operate.

Here is another maze.
It is more difficult than the first.
It is difficult because the problem space is much larger. As you search it, you will become cognitively overloaded trying to remember where you have come from, where you are, where you are going, and what your options for moves are.
AND...you are needing to attend to all of these at the same time.
Good luck. You'll need it.
Either that...or some sub goals.
(maze from: https://www.mazes.org.uk/difficult-maze-01s.htm)

This is a repeat of the difficult maze.
Several sub goals are provided.
Make your way from one to the next..if you can.
The larger a problem space, the more that subgoals are useful, and the more that you may seek to include.
Still, the gap between subgoal 1 and 2, and then subgoal 2 and 3...may be too large.
The "Hobbits and Orcs" problem is based upon the fact the orcs like to eat hobbits and will do so at every opportunity. However, they will only ever do so when they outnumber hobbits.
Three hobbits and three orcs are travelling together and come to a river which they need to cross.
There is a boat available for this purpose, but it can only hold two creatures at a time. Remember, if at any stage there are more orcs than hobbits together on one side of the river, then those hobbits will be eaten.
The boat cannot be pushed across the river. It must have one or two creatures in it to cross.
Determine how all six creatures cross without any being eaten.
You may like to try this problem. You will likely find it challenging if you have not seen it before. However, for our purposes of discussing subgoals, you are now going to be given one.
Hint: You will be focussing on how to move the creatures from one side to the other, and thinking that you must always put one creature in the boat to take it "back" to the starting side. However, there is a step where you will need to put two creatures in the boat and return both of them to the starting side.
If you would like access to a solution, it is provided to the right, and comes from: http://cognitivepsychology.wikidot.com/problem-solving:hobbits-and-orcs.
Consider a conventional pack of playing cards plus a conventional die.
Five cards are drawn at random, and the die is rolled once.
You win if you have at least one Ace in your hand or throw a "6", or both of these events.
What is the probability that you win?
Hint (Subgoall): Calculate the probability that you lose.
The phrasing of this question focuses on winning - and there are many ways to win. You will be tempted to calculate the chance of having a single Ace in your hand, two Aces in your hand, three Aces in your hand, four Aces in your hand - and these probabilities will all need to be added together according to the rules of probability calculus.
Then there is the die to consider, which is fairly straight forward (1 in 6 chance for a "6"), but it needs to be considered in relation to the cards drawn.
The subgoal is indicating to calculate the probability that you lose. It reframes the question, and it is much is easier to calculate, because there is only one way to lose. To lose, every card has to be "not an Ace" and the die roll has to be "not 6".
Without going into the finer details, once you calculate the probability of losing, the probability of you winning is as easy as subtracting your answer for losing from 1.
Kalyuga, S (2010). Schema acquisition and sources of cognitive load. In Jan L. Plass, Roxana Moreno & Roland Bruken (Eds.), Cognitive Load Theory: USA: Cambridge University Press, p48-64.
