The Goal-free Effect

Summary: 
A goal-free problem presents a generalised goal such as “find the values of what you can”, rather than a specified goal such as “find the value of x”. The goal-free effect occurs when presenting goal-free problems results in greater learning than presenting goal-specific statements.
Dynamics: 

When novices engage in conventional problem solving, they use means-ends analysis which imposes a high cognitive load directed towards managing that process.

Presenting goal-free problems prevents the use of means-ends analysis because it omits any specified goal to work backwards from, which is typically done in implementing means-ends analysis.

Goal-free problem statements guide a learner’s attention to the features of recognising the problem type and on executing a forward-working ‘step’ using the data provided. Consequently, goal-free problems are more effective in promoting learning of how to solve problems than is conventional problem solving.

Due to the open-ended nature of goal free problem statements, the potential problem space expands rapidly in areas of numerous options for forward working ‘steps’, thus threatening cognitive overload.  Consequently, goal-free problem statements are only useful in contexts of a small problem space involving very few possible operators.

Strategy: 

Problems should be presented in a goal-free statement form requesting learners to “find what they can”, rather than to find the value of a specific goal.

Other wordings for the question are viable, provided it promotes the learner to use the information given to drive performance forward rather than focusing on any specific goal and then working backwards from that goal.  Examples include “use the given information to calculate the values of other variables”, and the minimalist statement “do something”.

Instructional Design: 

Goal free problems are likely misnamed because they are not really without goals, but they are of a very low level of goal specificity.  The essential feature is to prevent backwards working from the goals and to promote forwards working from the given information.

Conventional problems may become such “low goal specific problems” by removing all reference to specific goals such as "find the value of x", "calculate the distance between…", “how many years of compound interest  will it take to…" and so on.

Instead, phrase the questions along the open lines of “use the given information to determine other things”.

If problems are "goal free", then a problem solver has little option but to focus on the information provided (the given data) and to use it wherever possible. This induces a forwards working solution path similar to that generated by expert problem solvers.  Such forward working solutions impose very low levels of cognitive load and facilitate learning (Ayres, 1993).

Example 1: Algebra goal free problem

If y = x + 6, x = z + 3 and z = 6, find what you can.

 

Example 2: Kinematics goal free problem

A particle starts from rest and is accelerated at 12 m/s2 for 4.5 seconds.

Calculate what you can.

 

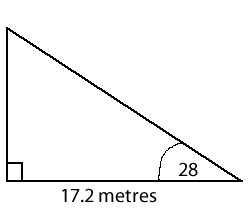
Example 3: Triangle geometry goal free problem

For the right triangle shown, find what you can.

 

 

 

 

References: 

Ayres PL, 1993, 'Why Goal-Free Problems Can Facilitate Learning', Contemporary Educational Psychology, vol. 18, no. 3, pp. 376 - 381, http://dx.doi.org/10.1006/ceps.1993.1027